Vamos aprender de forma prática os principais estilos de cobrança do Assunto PA e PG.
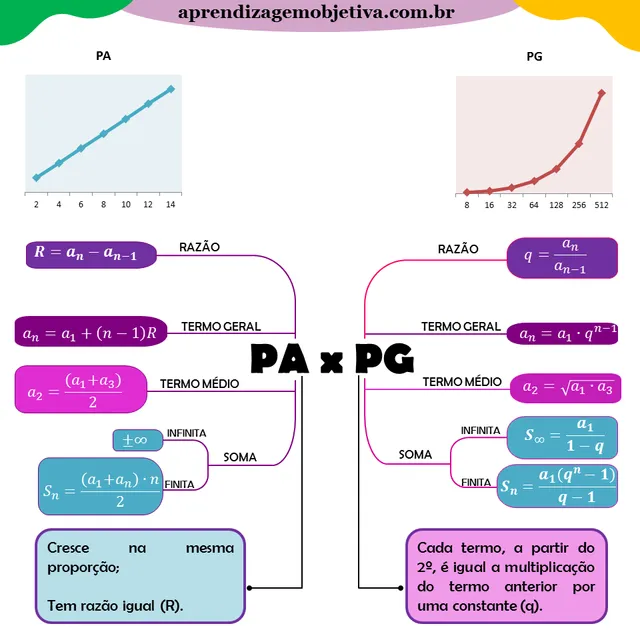
Antes de visualizar as questões comentadas, dê uma olhada neste resumo com as fórmulas de progressão geométrica e progressão aritmética mais cobradas em provas e concursos públicos. Memorizá-las será fundamental para ter um bom desempenho nas provas de PA e PG.
1 – (PREF. AMPARO/SP – AGENTE ESCOLAR – CONRIO/2014) Descubra o 99º termo da P.A.
(45, 48, 51,…)
A) 339
B) 337
C) 333
D) 331

2 – (CÂMARA DE SÃO PAULO/SP – TÉCNICO ADMINISTRATIVO – FCC/2014) Uma sequência inicia-se com o número 0,3. A partir do 2º termo, a regra de obtenção dos novos termos é o termo anterior menos 0,07. Dessa maneira o número que corresponde à soma do 4º e do 7º termos dessa sequência é:
A) -6,7.
B) 0,23.
C) -3,1.
D) -0,03.
E) -0,23.

3 – (BNDES – TÉCNICO ADMINISTRATIVO – CESGRANRIO/2013) Progressões aritméticas são sequências numéricas nas quais a diferença entre dois termos consecutivos é constante.
A sequência (5, 8, 11, 14, 17, …, 68, 71) é uma progressão aritmética finita que possui:
A) 67 termos
B) 33 termos
C) 28 termos
D) 23 termos
E) 21 termos

4 – A idade entre três irmãos formam uma P.A. Sabendo que o irmão mais novo tem 29 anos e o mais velho 41, qual é a idade do irmão do meio?

5 – A idade entre três irmãos formam uma P.A. Sabendo que a soma das três idades é 60, qual é a idade do irmão do meio?

7 – Calcule a soma dos 11 termos iniciais da P.G
(30,60,120,…)

8 – Calcule a soma dos 6 primeiros termos da PG (2, 6, 18, …):
A) Sn = 827.
B) Sn = 586.
C) Sn = 678.
D) Sn = 728.

9 – Observe a progressão geométrica (P.G.) e assinale o valor de y.
P.G. = (y + 30; y ; y – 60)
A) +30.
B) +60.
C) –30.
D) –60.
E) -90.

